Coronavirus: un modelo para predecir cuántas camas UCI harán falta durante cada oleada

La crisis financiera mundial de 2008 puso de moda en España el término económico “prima de riesgo”, hasta entonces desconocido. Del mismo modo, la pandemia ha popularizado expresiones y términos como “doblar la curva”, “incidencia acumulada” e incluso conceptos epidemiológicos más específicos como “el número efectivo de reproducción R₀”. Ocupan portadas de periódicos, así como espacios en noticiarios televisivos y radiofónicos. Constituyen una muestra del uso de las matemáticas para describir la evolución de la pandemia y para proporcionar indicadores con los que las autoridades políticas pueden fundamentar una toma de decisiones informada sobre medidas de distanciamiento social y restricciones a la movilidad.

Sin embargo, los modelos matemáticos no solo sirven para describir qué ha pasado o el estado actual de la pandemia, sino que pueden facilitar predicciones muy útiles sobre cómo va a evolucionar. Estas son útiles para la planificación de los recursos sanitarios necesarios para atender a paciente covid-19, como las camas UCI. La planificación facilita la utilización eficiente de recursos y, en consecuencia, proporcionar una mejor atención a todos los pacientes, covid y no covid.

Los modelos matemáticos más útiles para predecir variables relacionadas con la evolución de la pandemia son los de simulación. Estos modelos son capaces de representar características complejas de la realidad pandémica, como su aleatoriedad e incertidumbre, así como la variabilidad en el impacto que la enfermedad puede tener en distintas personas.

Modelos que simulan la actividad diaria de miles de individuos

Durante la pandemia se han popularizado algunos modelos de simulación basados en agentes, los cuales tratan de reproducir en el ordenador el comportamiento de un número muy elevado de personas (agentes) representativos de la sociedad de una región o país. Para ello, cada persona tiene creada (simulada) su red de contactos que reproducen los ámbitos familiares, de trabajo y social. Las personas están clasificadas en grupos que representan su estado en relación con la enfermedad.

La clasificación básica considera los grupos de infectados (y en disposición de contagiar), de susceptibles (que pueden ser contagiados) y de personas que ya han pasado la enfermedad y son inmunes o que han fallecido. El modelo matemático reproduce la dinámica diaria de contactos de cada agente y la posibilidad de contagio en cada uno de ellos para recrear la evolución global del número de personas contagiadas. Se trata de modelos que extienden, incorporando la aleatoriedad y la variabilidad citadas anteriormente, los modelos epidemiológicos compartimentales tipo SIR (susceptible-infected-removed).

Estos modelos, son muy útiles para evaluar las consecuencias de distintas políticas de distanciamiento social en la transmisión del virus y de distintas estrategias de vacunación en la población.

La dinámica hospitalaria reproducida por un modelo de simulación

Sin embargo, para predecir las necesidades de camas hospitalarias y de UCI son más adecuados modelos de simulación estocásticos de tipo mecanicista que se fundamentan en dar respuesta a las siguientes dos cuestiones:

• ¿Cuántos pacientes van a ingresar en el hospital cada uno de los próximos días?
  
• ¿Dónde y durante cuánto tiempo van a estar ingresados cada uno de estos pacientes?
  

La respuesta a la primera cuestión se consigue ajustando a la serie de datos de ingresos diarios de pacientes una curva que parte de cero, que experimenta un crecimiento exponencial, para posteriormente estabilizarse (en la llamada “meseta”) y finalmente decrecer de nuevo hacia cero.

Se utilizan curvas de crecimiento poblacional de tipo Gompertz, cuya derivada se muestra en la Figura 1. Con esta curva se estima cuántos pacientes, de media, van a ingresar cada uno de los días del futuro.

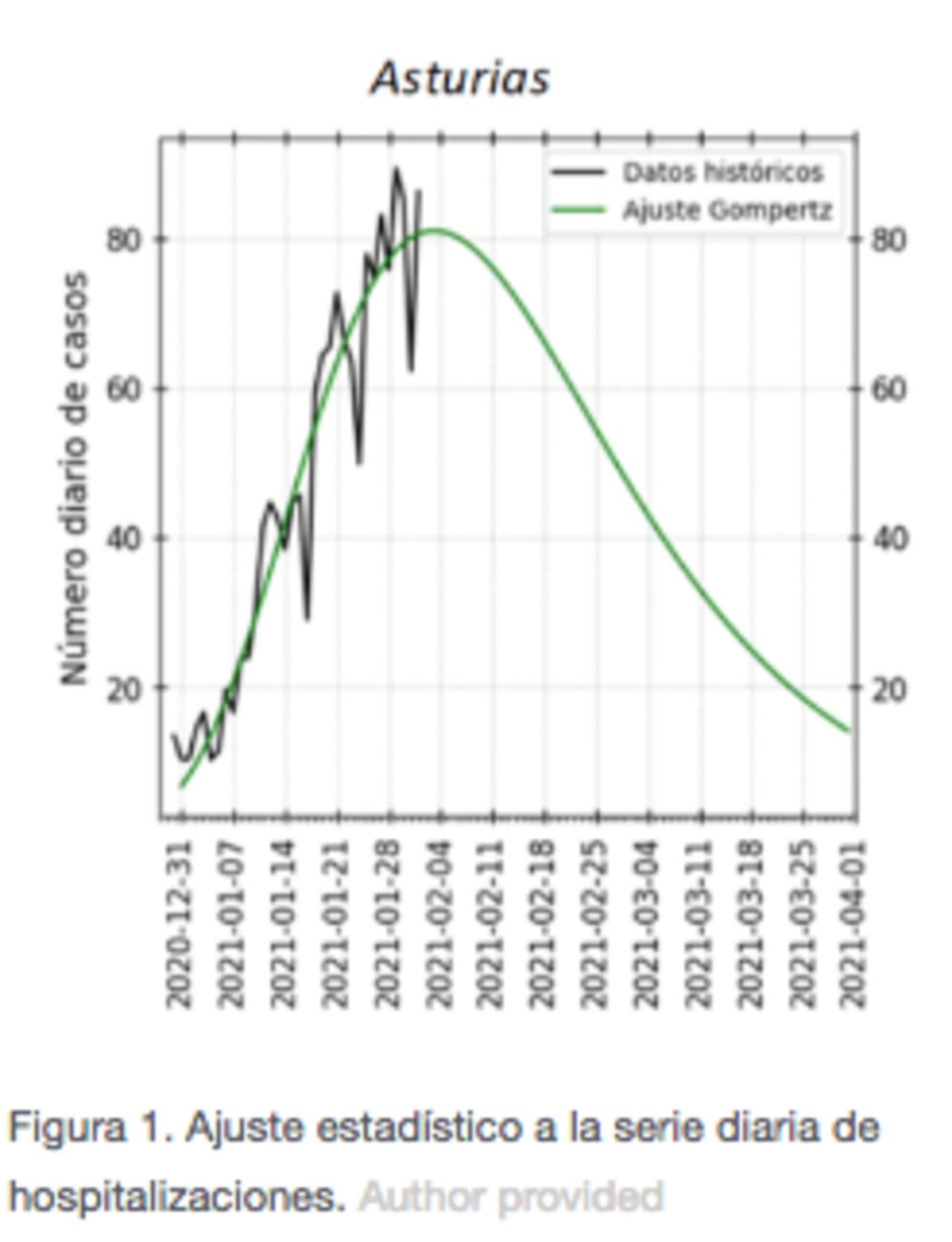
Una distribución de probabilidad de Poisson, con estos valores medios, facilita la simulación del número de pacientes (y con sus características de edad, sexo, etc.) que ingresa en el hospital cada día del futuro.

A la segunda cuestión se le da respuesta representando con precisión lo que ocurre puertas adentro del hospital (o conjunto de hospitales de una región).

La Figura 2 representa el flujo de pacientes por las instalaciones hospitalarias.

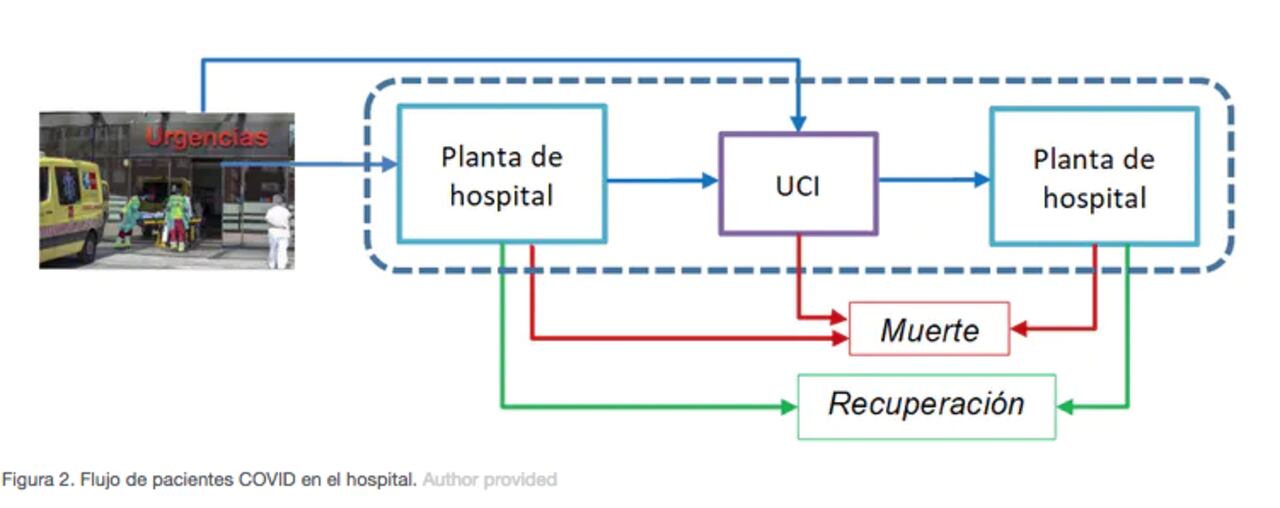
Un paciente COVID cuando ingresa en el hospital lo puede hacer directamente en UCI o bien en una planta para agudos. Desde aquí el paciente puede requerir un posterior ingreso en UCI, o bien ser dado de alta, por recuperación o por fallecimiento. Los pacientes que están ingresados en UCI pueden ser dados de alta bien por mejoría y terminar la recuperación en planta, o bien por fallecimiento.

En el gráfico se detallan todos los parámetros que son necesarios para recrear (simular) la trayectoria de un paciente COVID en el hospital: mediante letras “p” se denotan las probabilidades que determinan las trayectorias en las bifurcaciones y mediante letras mayúsculas, W, Y, X, los tiempos que el paciente permanece en las instalaciones.

Estos tiempos varían entre pacientes y son descritos mediante distribuciones de probabilidad que son estimadas, así como las probabilidades “p”, a partir de los datos observados en la evolución de la pandemia.

Predicción como resultado del análisis estadístico de miles de realidades futuras posibles

A partir del conocimiento de cuántos pacientes están actualmente hospitalizados y simulando llegadas futuras de pacientes y sus trayectorias hospitalarias se puede prever cuántas camas van a ser necesarias en las siguientes semanas de pandemia. La Figura 3 muestra el resultado de las predicciones y los valores reales observados realizados durante la primera ola pandémica en Navarra. Cada vez que se realiza una simulación se obtiene una realidad (de ocupación de camas) distinta para el futuro.

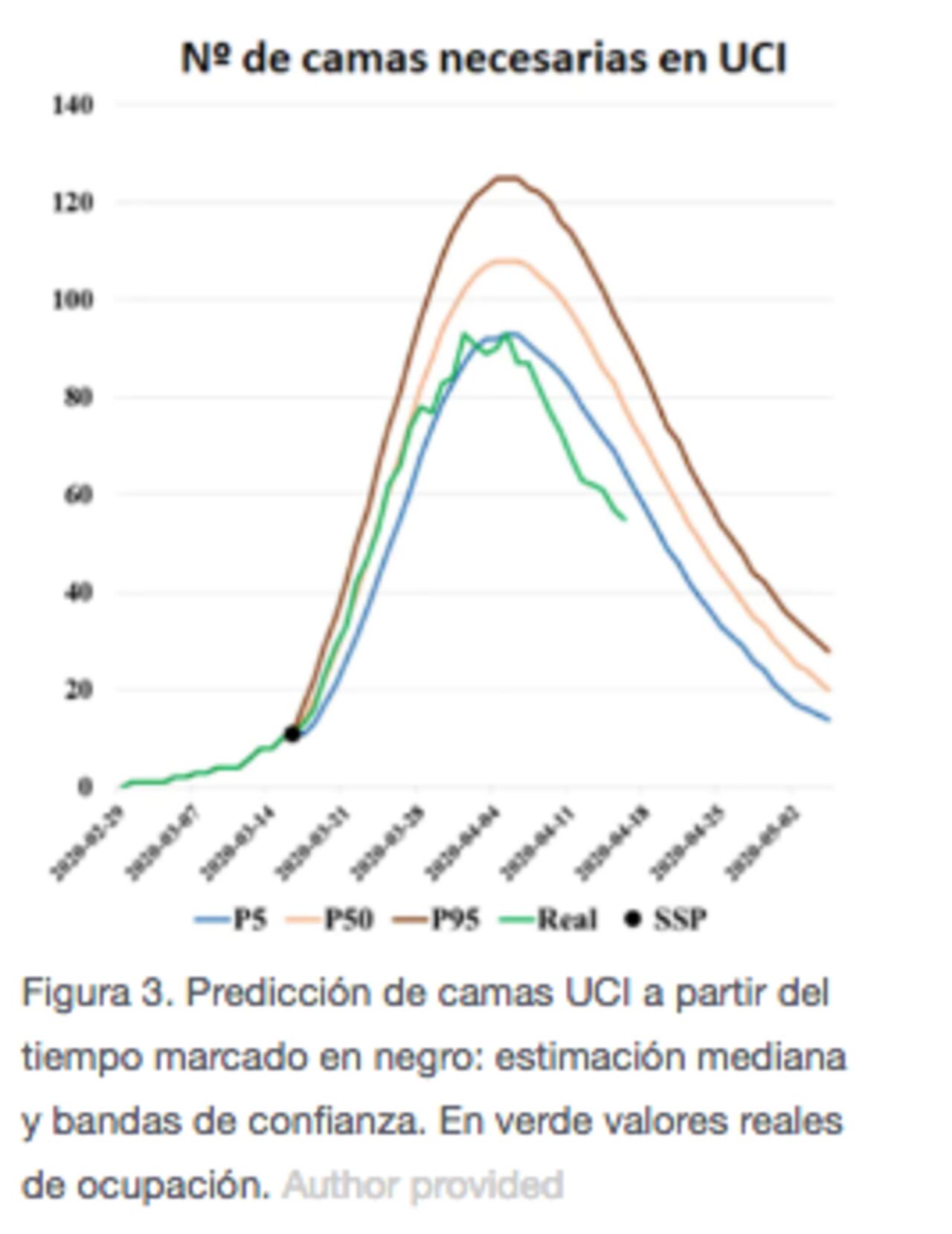
Del análisis estadístico de miles de esos posibles futuros resultan las predicciones medias y unas bandas de confianza. Modelos útiles en la práctica que sólo necesitan cuatro fechas por paciente

Este modelo de simulación ha sido utilizado durante las tres últimas olas pandémicas en Navarra y durante la segunda y tercera en La Rioja por los responsables de la planificación hospitalaria. El Ministerio de Sanidad español también ha recibido informes diarios de previsión de ocupación hospitalaria durante la duración de la tercera ola.

Los datos guían la calibración y actualización continua (aprendizaje) del modelo de simulación. Únicamente cuatro fechas por paciente, registradas por los sistemas de información hospitalarios, son necesarias para la construcción y ejecución del modelo: ingreso y alta hospitalaria, e ingreso y alta en UCI (en caso de producirse).

Este reducido conjunto de datos necesarios, y su disponibilidad en tiempo (casi) real en los sistemas de información hospitalarios, constituye uno de los puntos fuertes del modelo matemático en comparación con otros que precisan del conocimiento de multitud de parámetros y distribuciones de probabilidad que no están disponibles en tiempo real, y que, en todo caso, pueden ser estimados una vez que la pandemia ha pasado.

Sin duda, esta aplicación constituye una muestra más de la aportación que pueden realizar las matemáticas para mitigar los efectos de la pandemia. Otras aplicaciones de las matemáticas pueden encontrarse en la página web de la acción matemática contra el coronavirus y en la página web del grupo de investigación q-UPHS.

Por:

Fermín Mallor Giménez

Catedrático de Estadística e Investigación Operativa, Universidad Pública de Navarra

Daniel García de Vicuña Bilbao

Estudiante de doctorado en el Instituto de Smart Cities, Universidad Pública de Navarra

Artículo publicado originalmente en The Conversation